ひずみマッピング
材料の機械的特性と電気的特性は、その原子間間隔の変化(ひずみ)に直接関連しています。透過型電子顕微鏡 (TEM) では、無歪のリファレンスとなる領域と測定を行いたい箇所の面間隔 (d) を比較することによって結晶格子の変形を測定することが可能です(概要はこちらを参照ください、MRS Bulletin, 39, 138-146, 2014).
像観察による手法 (例えば、高分解能TEM (HRTEM) や高分解能STEM (HRSTEM) )を用いて面間距離 (d) を測定したり、電子線回折法 (例えば、ナノビーム電子線回折(NBED) )を用いて逆空間の距離 (g=1/d) を測定することが出来ます。
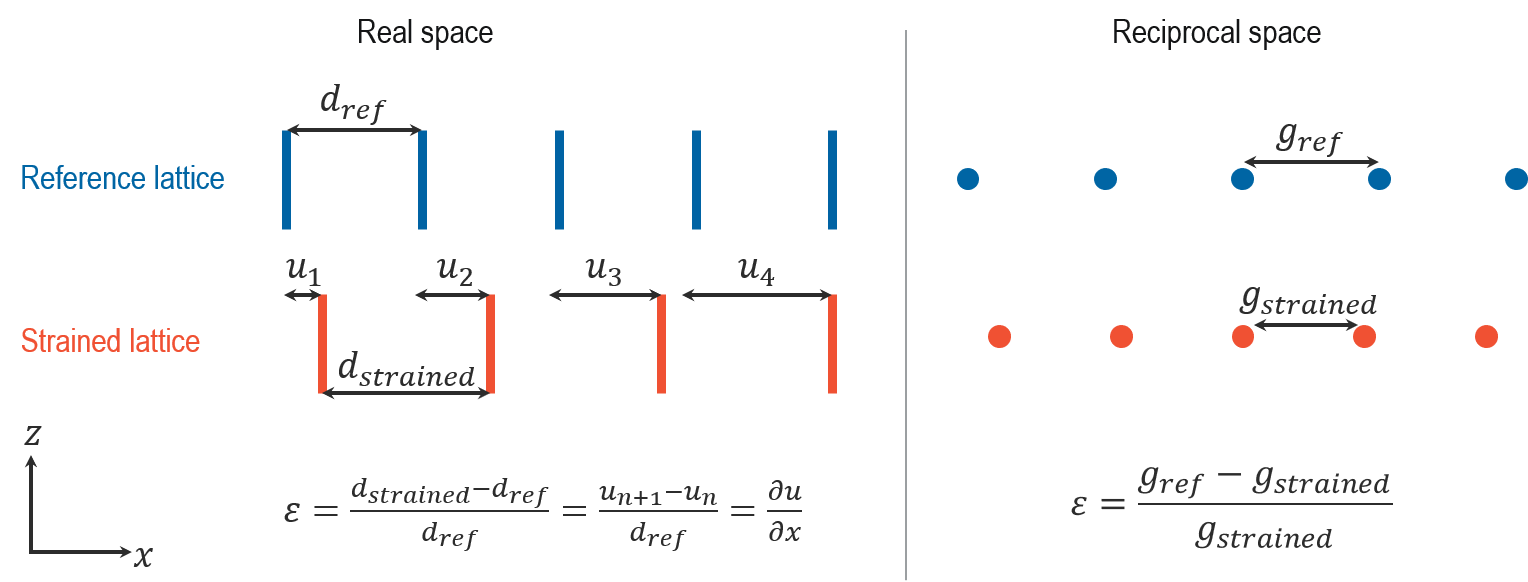
TEMのこれらの手法によって結晶格子の変形の二次元の測定結果が得られ、2×2の行列を用いて表現することが出来ます。その結果、二次元のひずみマップを下記に示すように計算することが可能です:
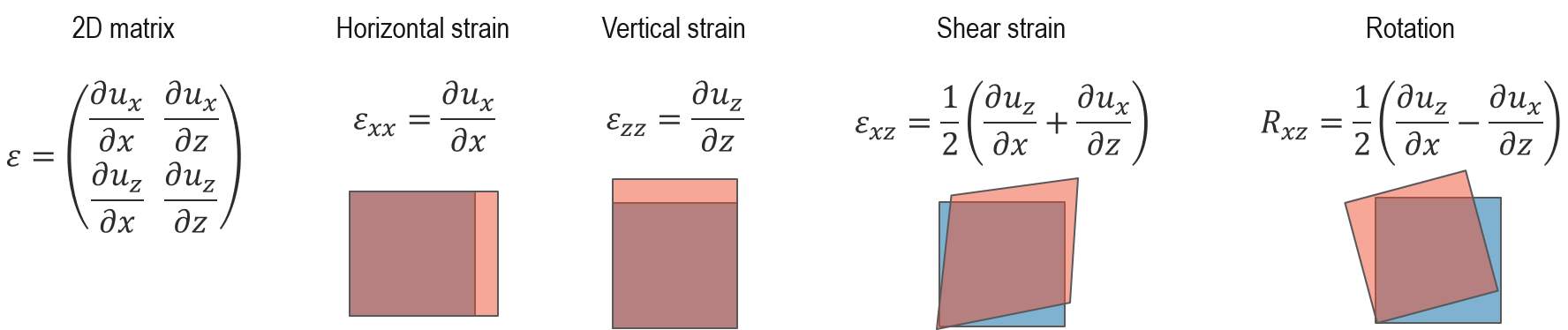
特に4D STEMを用いることで、ひずみを二つの方法で測定することが出来ます:
- CBED: 高次ラウエゾーン(HOLZ)の構造を詳細に測定します。この手法を行う場合、特定の方位へ試料を傾斜する必要があり、試料の厚さの範囲に制約があります。
- NBED: 原子間隔と回折スポットの間で反比例の関係にあることを利用します。
原子間隔と回折スポットの間で反比例の関係にあることを利用します。
NBEDを用いたひずみマッピングはその視野が単一の晶帯軸によく合っている必要はありませんが、実空間と逆空間のそれぞれの分解能の間でバランスし最適化されている必要があります。
- 大きな収束角(小さなSTEMプローブ径):空間分解能は改善しますが、ひずみ測定の精度は低下します。
- 小さな収束角(大きなSTEMプローブ径):ひずみ測定の精度は向上しますが、空間分解能は低下します。
メモ:4D STEMを用いたひずみ測定は結晶材料に限らず、非晶質材料や準結晶材料への適用も可能です (Applied Physics Letters, 112, 171905, 2018).
DigitalMicrographソフトウェアにおける4D STEMを用いたひずみマッピング
DigitalMicrograph®STEMx® は、NBEDデータを用いたひずみ測定と同一の原理を採用しており、下記のフローチャートに従っています。
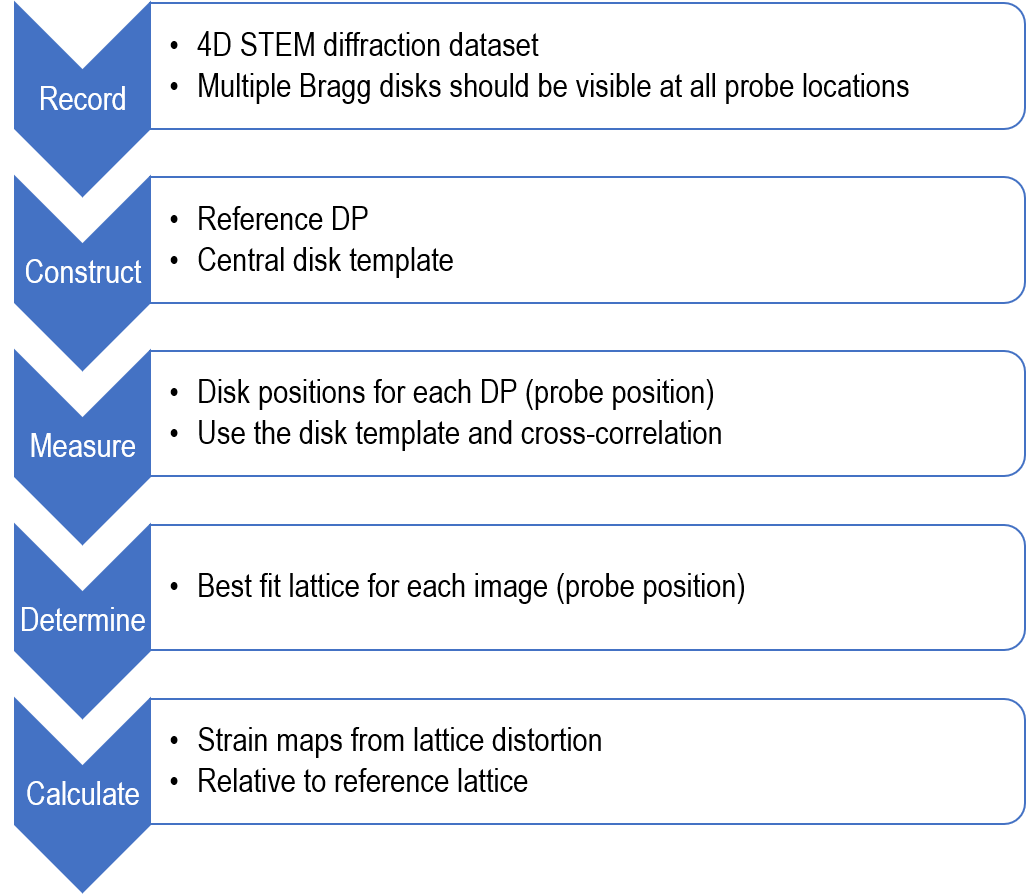
ひずみマッピングのための4D STEMデータ取得のポイント
二次元のひずみマッピングデータを取得する上で、試料と電子顕微鏡の設定が非常に重要です。この手法では、ディスク内は少ないコントラストでありながら同時にそのディスクの縁はシャープであり、同時にお互いに重なり合わない回折ディスクの二次元の列が必要です。
収束角: 収束角(コンデンサー絞り径とレンズの設定に依存)が空間分解能を決定します。より大きな収束角を設定することでより小さなSTEMプローブ径が得られ(より高い空間分解能)、またその逆も当てはまります。
カメラ長: カメラ上で2次から3次までの回折ディスクが観察されるようにカメラ長を選択します。より長いカメラ長を選択することでディスクをより多くのピクセルで記録することが可能となりますが(ディスクのフィッティングにおいてはプラスで望ましい)、カメラの各ピクセルに対する信号量は減少します(ディスクのフィッティングにおいてはマイナス)。収束角を設定する際にもこの点は注意する必要があります。
試料厚さと方位: 非弾性散乱(多すぎると回折ディスク内に構造が観察され、ディスクへのフィッティング精度が低下します)が生じない範囲で、適当な量の散乱がある試料の厚さを選択します(応力の緩和が無い範囲で)。
その他の注意: エネルギーフィルタ 4D STEM によって非弾性散乱電子による影響を押さえ、ひずみマッピングの測定結果を大きく改善します。
非弾性散乱電子を除去することによってコントラストが改善し、回折図形中の全てのラインと構造が観察されるようになります。
ひずみ計算
ここで示す試料のデータは、ドイツのエルンスト・ルスカ ・センターの研究者によって提供頂いたものを使用しました。
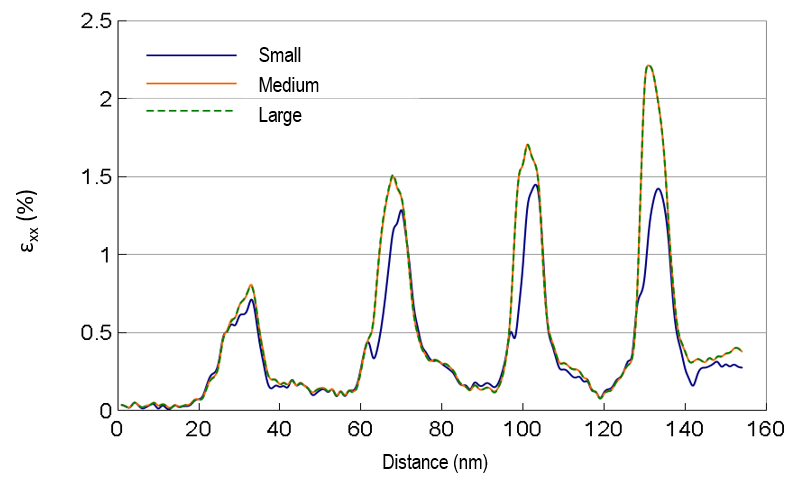
試料はGe濃度の異なるSiGe (21%、31%、38%、45%)の4層から成るSi/SiGe多層構造です。転位の全く無いエピタキシアル成長で成膜しています。Geの格子定数(0.5658 nm)はSiのそれ(0.5431 nm) よりも大きいため、Y方向(成長方向)に正のひずみが、X方向(面内方向)にはひずみがゼロであることが予想されます。シミュレーションによると、Y方向のひずみはGe濃度と共に増加することが予想されています(Geの最高濃度において最大3%)。
4D STEMのデータは、STEMプローブ径が約3 nmで収束角(半値)が0.6 mradで取得しています。回折図形を十分なシグナルノイズ比で取得するために、2次の回折スポットまで含まれるようにカメラ長を選択しました。
![]()
DigitalMicrographソフトウェアにおけるひずみ計算
DigitalMicrographソフトウェアにおけるひずみ計算は、Strain Mappingのパレット(スクリーンショットを示します)を用いて上記のフローチャートに従って4D STEMの回折図形データ(NBED)に対して行われます。
- リファレンスパターンの設定
第一のステップは、無歪の試料中の領域からリファレンスとなる回折図形を定義することです。上記の例ではSi基板を利用します。DigitalMicrographソフトウェアでは、選択した無歪の領域(像N)中の全てのピクセルの位置から得られる平均の回折図形を計算します。そしてこの図形に三つの赤い丸(Center、u、v単位ベクトルの選択)とひとつの緑色の円(Spots-スポットを探索する領域選択)が表示されます。
メモ:試料上で無歪の領域を指定しなかった場合には、リファレンスとなる回折図形は視野全体から生成します。このことは、ひずみの計算が(必ずしもひずみの無いとは限らない)平均値のリファレンスを用いて行われることを意味し、結果として値は絶対値とはなりません。
リファレンスパターンでは、以下の点を念頭に置いていくつかのパラメータを設定します。
- 単位ベクトルの選択:リファレンスとなる回折図形上の三つの赤い円を用いて、透過波(Center)と単位ベクトル(uとv)を指定します。また、これらはサーチする範囲内の残りの回折スポットを検出するためのテンプレートを生成するために使用されます。
- Centerの円は通常回折図形中央の透過波上に配置します。円の径は回折ディスクのテンプレートを生成するために用いる範囲を設定するため、他の回折ディスクに近づき過ぎない大きさで、観察されるディスクの周囲にマージンを取った十分な径で設定します。
- uとvの円はひずみが計算される結晶学的な方向に沿って配置します(例えば、面内と結晶成長方向など)。これらの円の径は全ての回折図形を分析してスポットの中心を検出する際に使用するサーチ半径を設定します。
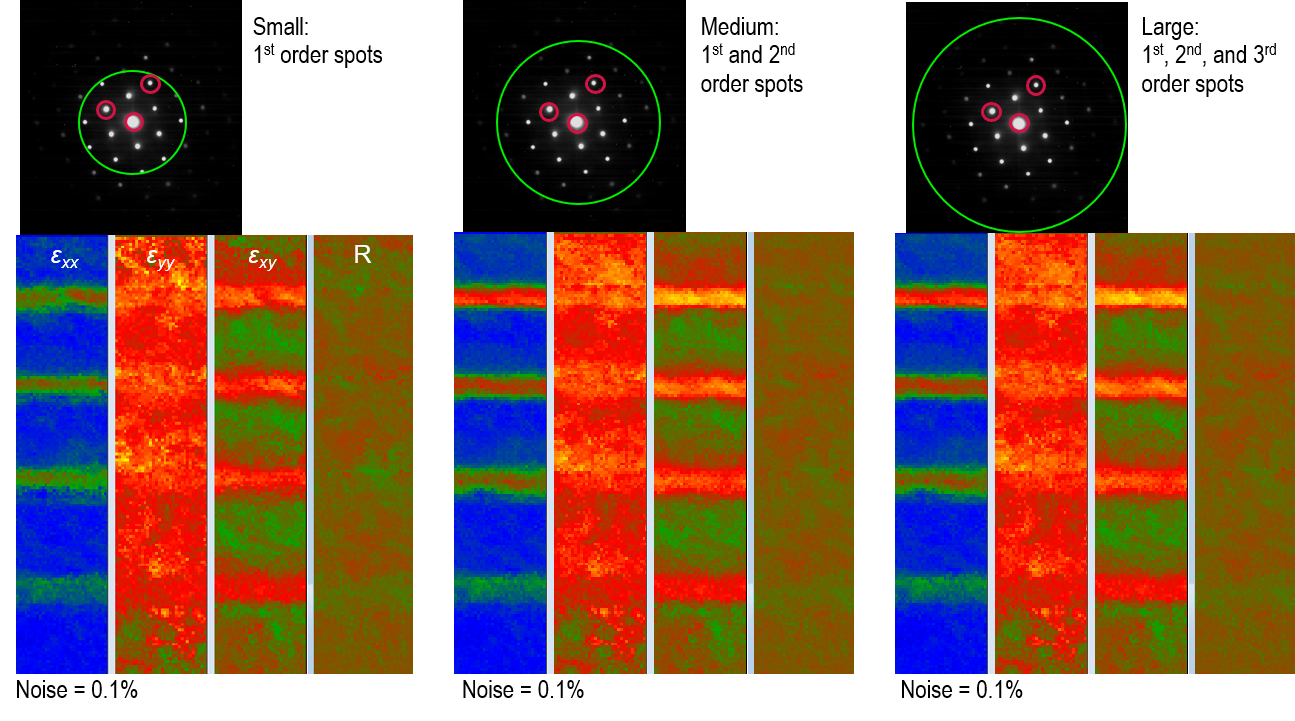
メモ:下記に示すように、高次の回折スポットを選択することによって、uとvの単位ベクトルが長くなります。このことは低次の回折スポットがひずみの計算において除外されることを意味し、結果として得られるひずみマップではノイズが大きくなります。
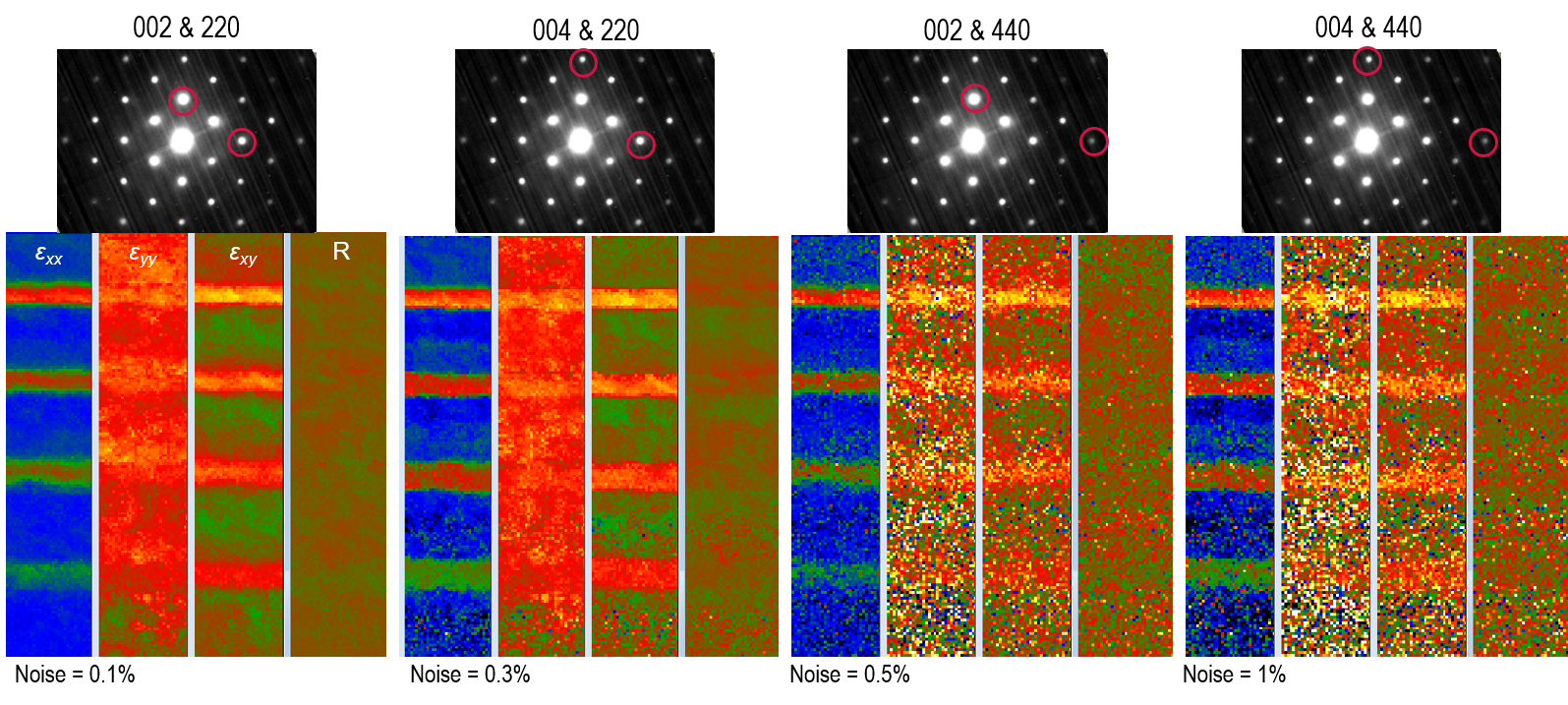
スポットの探索範囲の選択:DigitalMicrographソフトウェアでは、緑色のSpot円で選択した範囲内の回折スポットのみ探索します。より小さな径を選択することで各回折図形の探索範囲も小さくなり、ひずみ計算がスピードアップします。一方で、この径はこの計算に用いる回折スポットの次数を設定します。下記に示すようにこの設定によってノイズはあまり影響を受けませんが、計算に高次のスポットを含ませることによって、シミュレーションからこの試料で予想されるひずみの値により近い結果が得られています(ひずみはGe濃度と共に増加する)。
- ディスクテンプレートの生成
リファレンスとなる回折図形上で指定した透過波を用いて、データセット中の全ての回折ディスクの形状を反映したテンプレートを生成します。ひずみを計算するための各STEMプローブ位置における回折図形上のすべてのスポットの位置を検出するため、uとvの基本ベクトルの方向に沿ってこのテンプレート(上記のスクリーンショットでは像E)を用いています。
- ひずみマップの計算
全てのパラメータが設定されたので、ひずみマップの計算を行うことが出来ます。DigitalMicrographソフトウェアでは、各回折図形(各プローブ位置)に対して最もフィットする格子面を計算するため、ここまでの2ステップで得られたuとvの基本ベクトルとディスクテンプレートを使用しています。ひずみはリファレンスとなる格子と比較することで格子の変形量を計算しています(背景の節を参照してください)。注意すべき他の点としては:
- 現在の機能では、DigitalMicrographソフトウェアは回折図形上の垂直と水平方向に沿った投影のひずみ量を計算しています。これはuとvベクトルで定義される結晶学的な方向ではありません。そのため、実験中の回折図形の回転角を計測し、この値をひずみ計算前に回折図形に適用する回転角として入力することを勧めます。
- ひずみ計算において、特定のプローブ位置における回折スポットの散乱強度が小さい場合、DigitalMicrographソフトウェアはその回折パターンに対して解析を行わず、その位置のひずみ成分は全てゼロに設定されます。
先に述べたように、回折スポットの位置の正確な決定がこれらの測定に対して重要です。現在、DigitalMicrographソフトウェアではこの測定に相互相関法を採用しています。異なる相関法の比較については、Ultramicroscopy 176 (2017) 170–176.を参照してください。
謝辞
J. Ciston and C. Ophus (National Center for Electron Microscopy, CA, United States) consulted on the development of the strain mapping technique in DigitalMicrograph. We would also like to thank T. Denneulin and V. Migunov (Ernst Ruska Center for Microscopy and Spectroscopy with Electrons, Germany) for providing this dataset, figures, and discussions on parameter optimization for strain calculations.